在平面直角坐标系xOy中，经过点(0，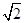
)且斜率为k的直线l与椭圆
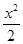＋y2＝1有两个不同的交点P和Q.
(1)求k的取值范围；
(2)设椭圆与x轴正半轴、y轴正半轴的交点分别为A，B，是否存在常数k，使得向量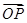
＋
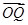与
共线？如果存在，求k的值；如果不存在，请说明理由．
相关试题
中，
，
，中心
在第一象限内，且与
轴的距离为一个单位，动点
沿矩形一边
运动，求
的取值范围．
的顶点
，求
的外接圆方程．
与圆
相交于两个不同点
，当
取不同实数值时，求
中点的轨迹方程．
，
是一个圆一条直径的两个端点，
是与
与
，点
且
为坐标原点．
相切时，求
面积最小，求直线推荐套卷
在平面直角坐标系xOy中，经过点(0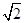，)且斜率为k的直线l与椭圆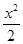＋y2＝1有两个不同的交点P和Q.
(1)求k的取值范围；
(2)设椭圆与x轴正半轴、y轴正半轴的交点分别为A，B，是否存在常数k，使得向量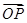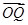＋与共线？如果存在，求k的值；如果不存在，请说明理由．
粤公网安备 44130202000953号