如图所示，在多面体ABCDEFG中，平面ABC∥平面DEFG，AD⊥平面DEFG，BA⊥AC，ED⊥DG，EF∥DG，且AC＝1，AB＝ED＝EF＝2，AD＝DG＝4.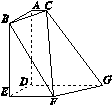
(1)求证：BE⊥平面DEFG；
(2)求证：BF∥平面ACGD；
(3)求二面角F－BC－A的余弦值．
．求
的最大值及最小正周期.
R
.
的最小正周期;
的值．
，
， 
⊥
, 且－＜
＜． 求
|
的最大值和最小值．
在区间
上的图像．相关知识点
推荐套卷
如图所示，在多面体ABCDEFG中，平面ABC∥平面DEFG，AD⊥平面DEFG，BA⊥AC，ED⊥DG，EF∥DG，且AC＝1，AB＝ED＝EF＝2，AD＝DG＝4.
(1)求证：BE⊥平面DEFG；
(2)求证：BF∥平面ACGD；
(3)求二面角F－BC－A的余弦值．
粤公网安备 44130202000953号