已知函数f(x)＝aln(2x＋1)＋bx＋1.
(1)若函数y＝f(x)在x＝1处取得极值，且曲线y＝f(x)在点(0，f(0))处的切线与直线2x＋y－3＝0平行，求a的值；
(2)若b＝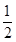
，试讨论函数y＝f(x)的单调性．
为
的外心，以线段
为邻边作平行四边形，第四个顶点为
,再以
为邻边作平行四边形，它的第四个顶点为
.
,试用
表示
；
；
外接圆的半径为
，用
.
中，
，求
的值.
，
为线段
上的一点，且有
，求点
求
的值
求
的范围相关知识点
推荐套卷
已知函数f(x)＝aln(2x＋1)＋bx＋1.
(1)若函数y＝f(x)在x＝1处取得极值，且曲线y＝f(x)在点(0，f(0))处的切线与直线2x＋y－3＝0平行，求a的值；
(2)若b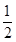＝，试讨论函数y＝f(x)的单调性．
粤公网安备 44130202000953号