若两个椭圆的离心率相等，则称它们为“相似椭圆”．如图，在直角坐标系xOy中，已知椭圆C1：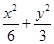
＝1，A1，A2分别为椭圆C1的左、右顶点．椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”．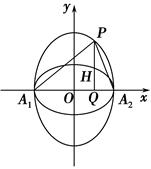
(1)求椭圆C2的方程；
(2)设P为椭圆C2上异于A1，A2的任意一点，过P作PQ⊥x轴，垂足为Q，线段PQ交椭圆C1于点H.求证：H为△PA1A2的垂心．(垂心为三角形三条高的交点)
.=
，求角A；
）.若
，且
，求角
的大小；推荐套卷
若两个椭圆的离心率相等，则称它们为“相似椭圆”．如图，在直角坐标系xOy中，已知椭圆C1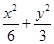：＝1，A1，A2分别为椭圆C1的左、右顶点．椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”．
(1)求椭圆C2的方程；
(2)设P为椭圆C2上异于A1，A2的任意一点，过P作PQ⊥x轴，垂足为Q，线段PQ交椭圆C1于点H.求证：H为△PA1A2的垂心．(垂心为三角形三条高的交点)
粤公网安备 44130202000953号