已知椭圆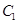 :
: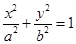 的离心率为
的离心率为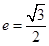 且与双曲线
且与双曲线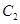 :
: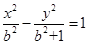 有共同焦点.
有共同焦点.
(1)求椭圆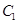 的方程;
的方程;
(2)在椭圆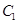 落在第一象限的图像上任取一点作
落在第一象限的图像上任取一点作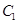 的切线
的切线 ,求
,求 与坐标轴围成的三角形的面积的最小值;
与坐标轴围成的三角形的面积的最小值;
(3)设椭圆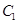 的左、右顶点分别为
的左、右顶点分别为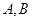 ,过椭圆
,过椭圆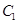 上的一点
上的一点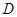 作
作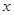 轴的垂线交
轴的垂线交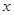 轴于点
轴于点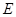 ,若
,若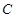 点满足
点满足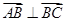 ,
,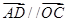 ,连结
,连结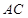 交
交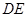 于点
于点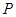 ,求证:
,求证: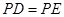 .
.
推荐套卷
已知椭圆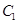 :
: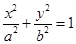 的离心率为
的离心率为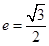 且与双曲线
且与双曲线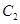 :
: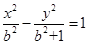 有共同焦点.
有共同焦点.
(1)求椭圆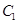 的方程;
的方程;
(2)在椭圆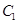 落在第一象限的图像上任取一点作
落在第一象限的图像上任取一点作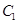 的切线
的切线 ,求
,求 与坐标轴围成的三角形的面积的最小值;
与坐标轴围成的三角形的面积的最小值;
(3)设椭圆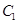 的左、右顶点分别为
的左、右顶点分别为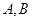 ,过椭圆
,过椭圆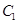 上的一点
上的一点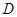 作
作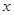 轴的垂线交
轴的垂线交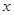 轴于点
轴于点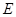 ,若
,若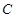 点满足
点满足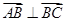 ,
,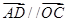 ,连结
,连结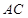 交
交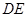 于点
于点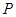 ,求证:
,求证: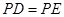 .
.