在直角坐标系xOy中，椭圆C的参数方程为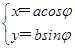
(φ为参数，a>b>0)，在极坐标系(与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴)中，直线l与圆O的极坐标方程分别为ρsin(θ＋
)＝
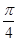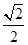m(m为非零数)与ρ＝b.若直线l经过椭圆C的焦点，且与圆O相切，求椭圆C的离心率．
相关试题
在
取得极值
的单调区间（用
表示）；
，
，若存在
，使得
成立，求
, 其中
.
时，求曲线
在点
处的切线方程；
时，求曲线
，数列
的项满足：
，（1）试求
的通项，并利用数学归纳法证明.
在
上单调，求
的值；
上的最大值是
，求
是虚数，
是实数，且
，那么
是否是纯虚数？并说明理由。推荐套卷
在直角坐标系xOy中，椭圆C的参数方程为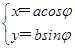 (φ为参数，a>b>0)，在极坐标系(与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴)中，直线l与圆O的极坐标方程分别为ρsin(θ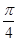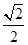＋)＝m(m为非零数)与ρ＝b.若直线l经过椭圆C的焦点，且与圆O相切，求椭圆C的离心率．
粤公网安备 44130202000953号