己知椭圆C：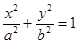
（a＞b＞0）的右焦点为F（1，0），点A（2，0）在椭圆C上，过F点的直线
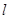与椭圆C交于不同两点
.
（1）求椭圆C的方程；
（2）设直线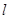斜率为1，求线段
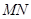的长；
（3）设线段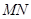的垂直平分线交
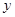轴于点P（0，y0），求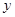的取值范围.
，B＝{x|x2－2x－m<0}，
推荐套卷
己知椭圆C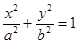：（a＞b＞0）的右焦点为F（1，0），点A（2，0）在椭圆C上，过F点的直线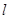与椭圆C交于不同两点.
（1）求椭圆C的方程；
（2）设直线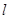斜率为1，求线段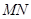的长；
（3）设线段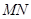的垂直平分线交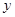轴于点P（0，y0），求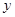的取值范围.
粤公网安备 44130202000953号