已知抛物线C:y2=2px(p>0),M点的坐标为(12,8),N点在抛物线C上,且满足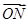 =
=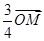 ,O为坐标原点.
,O为坐标原点.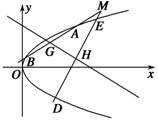
(1)求抛物线C的方程;
(2)以M点为起点的任意两条射线l1,l2的斜率乘积为1,并且l1与抛物线C交于A,B两点,l2与抛物线C交于D,E两点,线段AB,DE的中点分别为G,H两点.求证:直线GH过定点,并求出定点坐标.
相关知识点
推荐套卷
已知抛物线C:y2=2px(p>0),M点的坐标为(12,8),N点在抛物线C上,且满足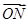 =
=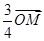 ,O为坐标原点.
,O为坐标原点.
(1)求抛物线C的方程;
(2)以M点为起点的任意两条射线l1,l2的斜率乘积为1,并且l1与抛物线C交于A,B两点,l2与抛物线C交于D,E两点,线段AB,DE的中点分别为G,H两点.求证:直线GH过定点,并求出定点坐标.