交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,
8)中度拥堵;T∈[8,10]严重拥堵,晚高峰时段,从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制直方图如图所示.
(1)这20个路段轻度拥堵、中度拥堵的路段各有多少个?
(2)从这20个路段中随机抽出的3个路段,用X表示抽取的中度拥堵的路段的个数,求X的分布列及期望.
相关知识点
推荐套卷
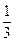 ,他们的投票相互没有影响.规定:若投票结果中至少有两张“同意”票,则决定对该项目投资;否则,放弃对该项目投资.
,他们的投票相互没有影响.规定:若投票结果中至少有两张“同意”票,则决定对该项目投资;否则,放弃对该项目投资.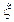 ,求
,求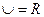 ,函数
,函数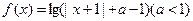 的定义域为A,集合
的定义域为A,集合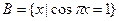 ,若
,若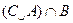 恰好有2个元素,求a的取值集合。
恰好有2个元素,求a的取值集合。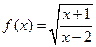 的定义域集合是A,
的定义域集合是A,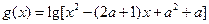 的定义域集合是B(1)求集合A、B(2)若A
的定义域集合是B(1)求集合A、B(2)若A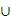 B=B,求实数
B=B,求实数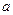 的取值范围.
的取值范围.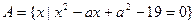 ,
,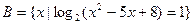 ,
,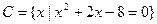 ,求a的值使
,求a的值使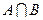 Æ,且
Æ,且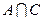 =Æ同时成立。
=Æ同时成立。 粤公网安备 44130202000953号
粤公网安备 44130202000953号