如图，D、E分别为△ABC的边AB、AC上的点，且不与△ABC的顶点重合。已知AE的长为
，AC的长为
,AD、AB的长是关于
的方程
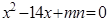的两个根。
（I）证明：C、B、D、E四点共圆；
（II）若∠A=90°，且
，求C、B、D、E所在圆的半径。
的大小；
平面
；
到平面
的距离。
上，且
，
为
的中点。
：
；
与
的长。
；
平面
。
且平行于平面
的一个截面，并说明理由；
推荐套卷
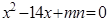如图，D、E分别为△ABC的边AB、AC上的点，且不与△ABC的顶点重合。已知AE的长为，AC的长为,AD、AB的长是关于的方程的两个根。
（I）证明：C、B、D、E四点共圆；
（II）若∠A=90°，且，求C、B、D、E所在圆的半径。
粤公网安备 44130202000953号