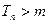已知在数列{an}中,a1=t,a2=t2,其中t>0,x=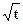 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1 (n≥2)的一个极值点(Ⅰ)求数列{an}的通项公式
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1 (n≥2)的一个极值点(Ⅰ)求数列{an}的通项公式
(Ⅱ)当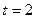 时,令
时,令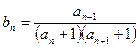 ,数列
,数列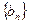 前
前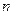 项的和为
项的和为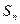 ,求证:
,求证: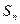

(Ⅲ)设 ,数列
,数列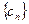 前
前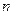 项的和为
项的和为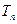 ,
, 求同时满足下列两个条件的
求同时满足下列两个条件的 的值:(1)
的值:(1)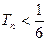 (2)对于任意的
(2)对于任意的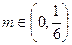 ,均存在
,均存在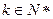 ,当
,当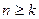 时,
时,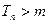
推荐套卷
已知在数列{an}中,a1=t,a2=t2,其中t>0,x=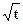 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1 (n≥2)的一个极值点(Ⅰ)求数列{an}的通项公式
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1 (n≥2)的一个极值点(Ⅰ)求数列{an}的通项公式
(Ⅱ)当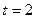 时,令
时,令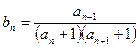 ,数列
,数列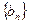 前
前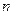 项的和为
项的和为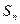 ,求证:
,求证: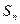

(Ⅲ)设 ,数列
,数列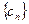 前
前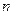 项的和为
项的和为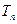 ,
, 求同时满足下列两个条件的
求同时满足下列两个条件的 的值:(1)
的值:(1)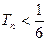 (2)对于任意的
(2)对于任意的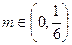 ,均存在
,均存在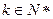 ,当
,当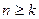 时,
时,