某工厂生产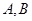 两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
 |
7 |
7 |
7.5 |
9 |
9.5 |
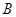 |
6 |
 |
8.5 |
8.5 |
 |
由于表格被污损,数据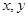 看不清,统计员只记得
看不清,统计员只记得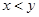 ,且
,且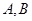 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.
(Ⅰ)求表格中 与
与 的值;
的值;
(Ⅱ)若从被检测的5件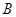 种元件中任取2件,求2件都为正品的概率.
种元件中任取2件,求2件都为正品的概率.
相关知识点
推荐套卷
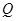 (简称血酒含量,单位是毫克/100毫升),当
(简称血酒含量,单位是毫克/100毫升),当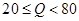 时,为酒后驾车;当
时,为酒后驾车;当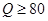 时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量(如下表).
时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量(如下表). 表示,醉酒驾车的人用小写字母如
表示,醉酒驾车的人用小写字母如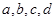 表示)
表示)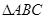 中,边
中,边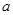 、
、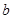 、
、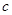 分别是角
分别是角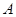 、
、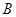 、
、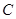 的对边,且满足
的对边,且满足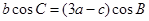 .
.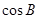 ;
;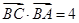 ,
,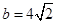 ,求边
,求边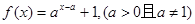 恒过定点
恒过定点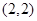 .
.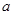 ;
;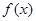 的图象向下平移1个单位,再向左平移
的图象向下平移1个单位,再向左平移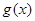 ,设函数
,设函数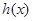 ,求
,求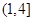 上的函数
上的函数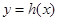 ,若在其定义域内,不等式
,若在其定义域内,不等式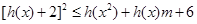 恒成立,求
恒成立,求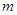 的取值范围.
的取值范围.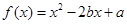 ,满足
,满足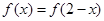 ,且方程
,且方程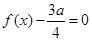 有两个相等的实根.
有两个相等的实根.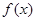 的解析式;
的解析式;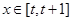
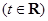 时,求函数
时,求函数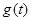 的表达式.
的表达式.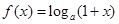 ,
,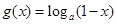 ,其中
,其中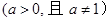 ,设
,设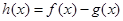 .
.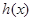 的定义域;
的定义域;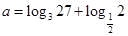 ,求使
,求使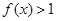 成立的
成立的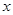 的集合.
的集合. 粤公网安备 44130202000953号
粤公网安备 44130202000953号