已知a,b为常数,a¹0,函数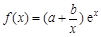 .
.
(1)若a=2,b=1,求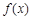 在(0,+∞)内的极值;
在(0,+∞)内的极值;
(2)①若a>0,b>0,求证: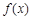 在区间[1,2]上是增函数;
在区间[1,2]上是增函数;
②若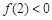 ,
,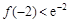 ,且
,且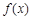 在区间[1,2]上是增函数,求由所有点
在区间[1,2]上是增函数,求由所有点 形成的平面区域的面积.
形成的平面区域的面积.
推荐套卷
已知a,b为常数,a¹0,函数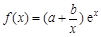 .
.
(1)若a=2,b=1,求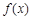 在(0,+∞)内的极值;
在(0,+∞)内的极值;
(2)①若a>0,b>0,求证: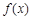 在区间[1,2]上是增函数;
在区间[1,2]上是增函数;
②若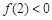 ,
,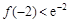 ,且
,且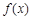 在区间[1,2]上是增函数,求由所有点
在区间[1,2]上是增函数,求由所有点 形成的平面区域的面积.
形成的平面区域的面积.