（本小题满分10分）通过点A（0，a）的直线
与圆
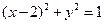相交于不同的两点B、C，在线段BC上取一点P，使
=
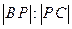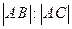，设点B在点C的左边，（1）试用a和k表示P点的坐标；（2）求k变化时P点的轨迹；（3）证明不论a取何值时，上述轨迹恒过圆内的一定点．
．
的最小正周期；
时，求函数
=
,
=
.
的值;
,
,求
的值.
、
、
是同一平面内的三个向量，其中
|
，且
，求
且
与
垂直，求
的最小正周期，最大值与最小值.
相关知识点
推荐套卷
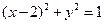（本小题满分10分）通过点A（0，a）的直线与圆相交于不同的两点B、C，在线段BC上取一点P，使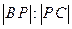=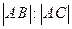，设点B在点C的左边，（1）试用a和k表示P点的坐标；（2）求k变化时P点的轨迹；（3）证明不论a取何值时，上述轨迹恒过圆内的一定点．
粤公网安备 44130202000953号