某园艺师用两种不同的方法培育了一批珍贵树苗,在树苗3个月大的时候,随机抽取甲、乙两种方法培育的树苗各10株,测量其高度,得到的茎叶图如图所示(单位:cm).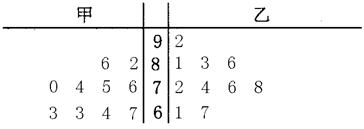
(Ⅰ)依茎叶图判断用哪种方法培育的树苗的平均高度大?
(Ⅱ)现从用两种方法培育的高度不低于80cm的树苗中随机抽取两株,求至少有一株是甲方法培育的概率。
相关知识点
推荐套卷
某园艺师用两种不同的方法培育了一批珍贵树苗,在树苗3个月大的时候,随机抽取甲、乙两种方法培育的树苗各10株,测量其高度,得到的茎叶图如图所示(单位:cm).
(Ⅰ)依茎叶图判断用哪种方法培育的树苗的平均高度大?
(Ⅱ)现从用两种方法培育的高度不低于80cm的树苗中随机抽取两株,求至少有一株是甲方法培育的概率。