如图,在11×11的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).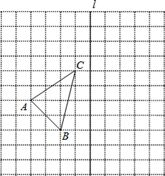
(1)在图中作出△ABC关于直线l对称的△A1B1C1;(要求A与A1,B与B1,C与C1相对应)
(2)作出△ABC绕点C顺时针方向旋转90°后得到的△A2B2C;
(3)在(2)的条件下求出线段CB旋转到CB2所扫过的面积.(结果保留π)
推荐套卷
如图,在11×11的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1;(要求A与A1,B与B1,C与C1相对应)
(2)作出△ABC绕点C顺时针方向旋转90°后得到的△A2B2C;
(3)在(2)的条件下求出线段CB旋转到CB2所扫过的面积.(结果保留π)