某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段: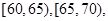
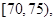

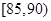 后得到如图4的频率分布直方图.
后得到如图4的频率分布直方图.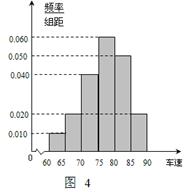
问:(1)求这40辆小型车辆车速的众数和中位数的估计值.(2)若从车速在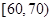 的车辆中任抽取2辆,求抽出的2辆车中车速在
的车辆中任抽取2辆,求抽出的2辆车中车速在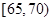 的车辆数
的车辆数 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).
推荐套卷
某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段: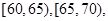
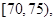

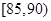 后得到如图4的频率分布直方图.
后得到如图4的频率分布直方图.
问:(1)求这40辆小型车辆车速的众数和中位数的估计值.(2)若从车速在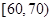 的车辆中任抽取2辆,求抽出的2辆车中车速在
的车辆中任抽取2辆,求抽出的2辆车中车速在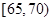 的车辆数
的车辆数 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).