(本小题满分12分)为迎接2014年“马”年的到来,某校举办猜奖活动,参与者需先后回答两道选择题,问题 有三个选项,问题
有三个选项,问题 有四个选项,但都只有一个选项是正确的,正确回答问题
有四个选项,但都只有一个选项是正确的,正确回答问题 可获奖金
可获奖金 元,正确回答问题
元,正确回答问题 可获奖金
可获奖金 元,活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答正确,则继续答题,否则该参与者猜奖活动终止,假设一个参与者在回答问题前,对这两个问题都很陌生.
元,活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答正确,则继续答题,否则该参与者猜奖活动终止,假设一个参与者在回答问题前,对这两个问题都很陌生.
(1)如果参与者先回答问题 ,求其恰好获得奖金
,求其恰好获得奖金 元的概率;
元的概率;
(2)试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大.
推荐套卷
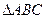 的内角A、B、C所对的边长分别为
的内角A、B、C所对的边长分别为 ,且
,且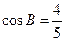 ,
,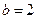 。
。 时,求
时,求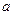 的值.
的值.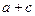 的值.
的值.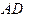 是
是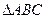 的外角
的外角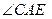 的平分线,交BC的延长线于点D,延长DA交
的平分线,交BC的延长线于点D,延长DA交
 .
. .
.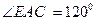 ,BC=6cm,求AD的长.
,BC=6cm,求AD的长. ,若存在
,若存在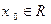 ,使得
,使得 成立,称
成立,称 为不动点,已知函数
为不动点,已知函数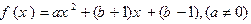
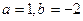 时,求函数
时,求函数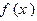 不动点.
不动点.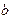 ,函数
,函数 作倾斜角为
作倾斜角为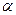 的直线与曲线
的直线与曲线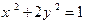 交于点
交于点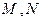 ,求
,求 最小值及相应的
最小值及相应的 粤公网安备 44130202000953号
粤公网安备 44130202000953号