今年疫情期间,针对各种入口处人工测量体温存在的感染风险高、效率低等问题,清华大学牵头研制一款“测温机器人”,如图1,机器人工作时,行人抬手在测温头处测量手腕温度,体温合格则机器人抬起臂杆行人可通行,不合格时机器人不抬臂杆并报警,从而有效阻隔病原体.

(1)为了设计“测温机器人”的高度,科研团队采集了大量数据.下表是抽样采集某一地区居民的身高数据:
|
测量对象 |
男性
岁) |
女性
岁) |
|
抽样人数(人
|
2000 |
5000 |
20000 |
2000 |
5000 |
20000 |
|
平均身高(厘米) |
173 |
175 |
176 |
164 |
165 |
164 |
|
|
|
|
|
|
|
|
根据你所学的知识,若要更准确的表示这一地区男、女的平均身高,男性应采用 176 厘米,女性应采用 厘米;
(2)如图2,一般的,人抬手的高度与身高之比为黄金比时给人的感觉最舒适,由此利用(1)中的数据得出测温头点
距地面105厘米.指示牌挂在两臂杆
,
的连接点
处,
点距地面110厘米.臂杆落下时两端点
,
在同一水平线上,
厘米,点
在点
的正下方5厘米处.若两臂杆长度相等,求两臂杆的夹角.
(参考数据表)
|
计算器按键顺序 |
计算结果(近似值) |
计算器按键顺序 |
计算结果(近似值) |
|
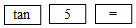
|
0.1 |

|
78.7 |
|

|
0.2 |

|
84.3 |
|

|
1.7 |
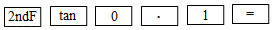
|
5.7 |
|

|
3.5 |
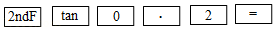
|
11.3 |