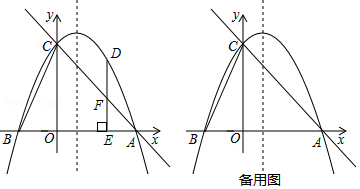
如图,抛物线 与 轴交于 , 两点,且 ,与 轴交于点 ,连接 ,抛物线对称轴为直线 , 为第一象限内抛物线上一动点,过点 作 于点 ,与 交于点 ,设点 的横坐标为 .
(1)求抛物线的表达式;
(2)当线段 的长度最大时,求 点的坐标;
(3)抛物线上是否存在点 ,使得以点 , , 为顶点的三角形与 相似?若存在,求出 的值;若不存在,请说明理由.
相关知识点
推荐套卷
如图,抛物线 与 轴交于 , 两点,且 ,与 轴交于点 ,连接 ,抛物线对称轴为直线 , 为第一象限内抛物线上一动点,过点 作 于点 ,与 交于点 ,设点 的横坐标为 .
(1)求抛物线的表达式;
(2)当线段 的长度最大时,求 点的坐标;
(3)抛物线上是否存在点 ,使得以点 , , 为顶点的三角形与 相似?若存在,求出 的值;若不存在,请说明理由.
