如图,四棱锥S-ABCD中,SD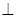 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD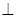 DC,AB=AD=1,DC=SD=2,E为棱SB上任一点.
DC,AB=AD=1,DC=SD=2,E为棱SB上任一点.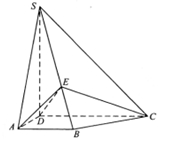
(Ⅰ)求证:无论E点取在何处恒有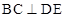 ;
;
(Ⅱ)设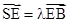 ,当平面EDC
,当平面EDC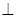 平面SBC时,求
平面SBC时,求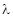 的值;
的值;
(Ⅲ)在(Ⅱ)的条件下求二面角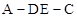 的大小.
的大小.
推荐套卷
如图,四棱锥S-ABCD中,SD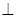 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD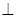 DC,AB=AD=1,DC=SD=2,E为棱SB上任一点.
DC,AB=AD=1,DC=SD=2,E为棱SB上任一点.
(Ⅰ)求证:无论E点取在何处恒有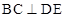 ;
;
(Ⅱ)设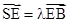 ,当平面EDC
,当平面EDC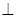 平面SBC时,求
平面SBC时,求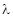 的值;
的值;
(Ⅲ)在(Ⅱ)的条件下求二面角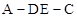 的大小.
的大小.