(本小题满分12分)f(x)=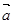 .
.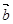 ,其中向量
,其中向量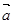 =(m,cos2x),
=(m,cos2x),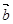 =(1+sin2x,1),
=(1+sin2x,1),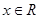 ,且函数
,且函数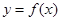 的图象经过点
的图象经过点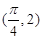 .
.
(Ⅰ)求实数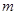 的值.
的值.
(Ⅱ)求函数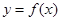 的最小值及此时
的最小值及此时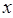 值的集合。
值的集合。
相关知识点
推荐套卷
(本小题满分12分)f(x)=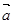 .
.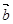 ,其中向量
,其中向量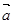 =(m,cos2x),
=(m,cos2x),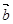 =(1+sin2x,1),
=(1+sin2x,1),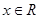 ,且函数
,且函数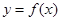 的图象经过点
的图象经过点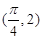 .
.
(Ⅰ)求实数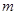 的值.
的值.
(Ⅱ)求函数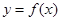 的最小值及此时
的最小值及此时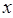 值的集合。
值的集合。