现有10道题，其中6道甲类题，4道乙类题，张同学从中任取3道题解答.
（I）求张同学至少取到1道乙类题的概率；
（II）已知所取的3道题中有2道甲类题，1道乙类题.设张同学答对甲类题的概率都是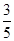
，答对每道乙类题的概率都是
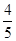，且各题答对与否相互独立.用
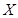表示张同学答对题的个数，求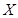的分布列和数学期望.
相关知识点
推荐套卷
现有10道题，其中6道甲类题，4道乙类题，张同学从中任取3道题解答.
（I）求张同学至少取到1道乙类题的概率；
（II）已知所取的3道题中有2道甲类题，1道乙类题.设张同学答对甲类题的概率都是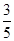，答对每道乙类题的概率都是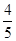，且各题答对与否相互独立.用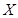表示张同学答对题的个数，求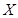的分布列和数学期望.
粤公网安备 44130202000953号