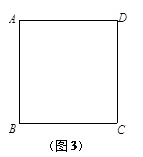探究一:如图1,已知正方形ABCD,E、F分别是BC、AB上的两点,且AE⊥DF.小明经探究,发现AE=DF.请你帮他写出证明过程.
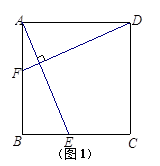
探究二:如图2,在矩形ABCD中,AB=3,BC=4,E、G分别在边BC、AD上,F、H分别在边AB、CD上,且GE⊥FH.小明发现,GE与FH并不相等,请你帮他求出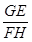 的值.
的值.
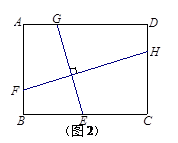
探究三:小明思考这样一个问题:如图3,在正方形ABCD中,若E、G分别在边BC、AD上,F、H分别在边AB、CD上,且GE=FH,试问:GE⊥FH是否成立?若一定成立,请给予证明;若不一定成立,请画图并作出说明.