某航空公司经营A、B、C、D四个城市之间的客运业务. 若机票价格y(元)是两城市间的距离x（千米）的一次函数. 今年“五、一”期间部分机票价格如下表所示：
（1）求该公司机票价格y（元）与距离x（千米）的函数关系式；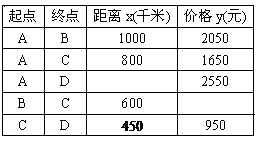
（2）利用（1）中的关系式将表格填完整；
（3）判断A、B、C、D这四个城市中，哪三个城市在同一条直线上？请说明理由；
（4）若航空公司准备从旅游旺季的7月开始增开从B市直接飞到D市的旅游专线，且按以上规律给机票定价，那么机票定价应是多少元？
相关试题
的外接圆，
， 
为⊙O的直径，BD=2，连结
，求BC的长. 
，点B为CD延长线上一点，且BD＝2AD．求AB的长.
已知二次函数
（1）用配方法将
化成
的形式；（2）在坐标系中利用描点法画出它的图象；
| x |
… |
… |
|||||
| y |
… |
… |
（3）根据图象回答：当自变量x的取值范围满足什么
条件时，
随着
的增大而减小？
与
轴的两个交点分别为A、B,点A在点B的左侧，与y轴交于点C，顶点为D，直线
经过点A、C．
为抛物线上的一个动点，求使得
的面积与
的面积相等的点相关知识点
推荐套卷
粤公网安备 44130202000953号