如图，在平面直角坐标系xOy中，抛物线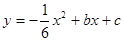
过点A(0，4)和C(8，0)，P(t，0)是
轴正半轴上的一个动点，M是线段AP的中点，将线段MP绕点P顺时针旋转90°得线段PB．过B作轴的垂线、过点A作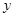
轴的垂线，两直线相交于点D．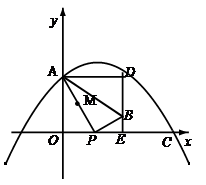
（1）求b、c的值；
（2）当t为何值时，点D落在抛物线上；
（3）是否存在，使得以A、B、D为顶点的三角形与△AOP相似？若存在，求此时的值；若不存在，请说明理由；
（4）连结AC，在点P运动过程中，若以PB为直径的圆与直线AC相切，直接写出此时t的值．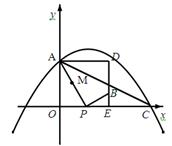
相关试题
与
的图像的交点的坐标为P（1，–2）．求:方程组
的解和b的值．如图，已知△ABC的三个顶点的坐标都在格点上，分别为A（－2,3）、B（－6,0） 、C（－1,0）．
（1）请将点A、B、C的纵坐标分别乘以-1后得到点A′、B′、C ′描在坐标系中，并顺次连接A′、B′、C ′得到△A′B′C ′；
（2）请问△A′B′C ′与△ABC有怎样的位置关系？
，
，
，…
=×；
下表给出了某班6名同学身高情况（单位：cm）
（1）完成表中空的部分；
（2）他们6人中最高身高比最矮身高高多少？
（3）如果身高达到或超过平均身高时叫达标身高，那么这6个同学身高的达标率是多少？（用小数表示，精确到小数点后两位）
相关知识点
推荐套卷
粤公网安备 44130202000953号