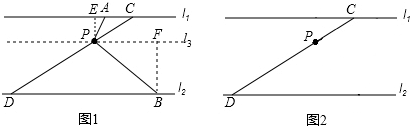(年湖北随州10分)已知两条平行线l1、l2之间的距离为6,截线CD分别交l1、l2于C、D两点,一直角的顶点P在线段CD上运动(点P不与点C、D重合),直角的两边分别交l1、l2与A、B两点.
(1)操作发现
如图1,过点P作直线l3∥l1,作PE⊥l1,点E是垂足,过点B作BF⊥l3,点F是垂足.此时,小明认为△PEA∽△PFB,你同意吗?为什么?
(2)猜想论证
将直角∠APB从图1的位置开始,绕点P顺时针旋转,在这一过程中,试观察、猜想:当AE满足什么条件时,以点P、A、B为顶点的三角形是等腰三角形?在图2中画出图形,证明你的猜想.
(3)延伸探究
在(2)的条件下,当截线CD与直线l1所夹的钝角为150°时,设CP=x,试探究:是否存在实数x,使△PAB的边AB的长为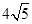 ?请说明理由.
?请说明理由.