如图，A、B两个村子在河CD的同侧，A、B两村到河的距离分别为AC＝1 km，BD＝3 km，CD＝3 km现在河边CD上建一水厂向A、B两村输送自来水，铺设水管的费用为20 000元／千米．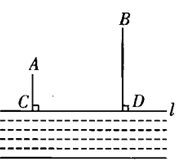
（1）请你在河CD边上作出水厂位置O，使铺设水管的费用最省；
（2）求出铺设水管的总费用．
相关试题
互为相反数，
互为倒数，
的倒数等于它本身，则
的值是多少？
,
，求
的值．
，其中
，
的值．
（2）
；
,
°,证明:
是等边三角形
推荐套卷
如图，A、B两个村子在河CD的同侧，A、B两村到河的距离分别为AC＝1 km，BD＝3 km，CD＝3 km现在河边CD上建一水厂向A、B两村输送自来水，铺设水管的费用为20 000元／千米．
（1）请你在河CD边上作出水厂位置O，使铺设水管的费用最省；
（2）求出铺设水管的总费用．
粤公网安备 44130202000953号