（1）学完全等三角形以后，老师布置了这样一道题：如图1，点M、N分别在等边△ABC的BC、CA边上，且BM=CN，AM、BN交于点Q．试说明：∠BQM=60°．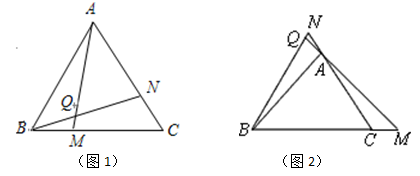
（2）小丽做完后，进行了反思，提出了许多问题，如：
①若将题中“BM=CN”与“∠BQM=60°”的位置交换，得到的是否仍是真命题？
②若将题中的点M、N分别移动到BC、CA的延长线上，是否仍能得到∠BQM=60°？
请你作出判断，在下列横线上填写“是”或“否”：① ；② ．
并对②给出证明．
相关试题
如图，过 外一点 作 的切线 切 于点 ，连接 并延长，与 交于 、 两点， 是半圆 的中点，连接 交 于点 ，连接 、 ．
（1）求证： ；
（2）若 ， ，求 的长．
如图所示，在平面直角坐标系中，一次函数 与反比例函数 的图象交于第二、四象限 、 两点，过点 作 轴于 ， ， ，且点 的坐标为 ．
（1）求一次函数与反比例函数的解析式；
（2） 是 轴上一点，且 是等腰三角形，请直接写出所有符合条件的 点坐标．
相关知识点
推荐套卷
粤公网安备 44130202000953号