A，B，C三个村庄在一条东西走向的公路沿线，如图所示，AB=2km,BC=3km,在B村的正北方向有一个D村，测得∠ADC=450今将△ACD区域规划为开发区，除其中4 km2的水塘外，均作为建筑或绿化用地，试求这个开发区的建筑及绿化用地的面积是多少？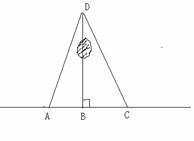
、
为实数，
求
相关知识点
推荐套卷
A，B，C三个村庄在一条东西走向的公路沿线，如图所示，AB=2km,BC=3km,在B村的正北方向有一个D村，测得∠ADC=450今将△ACD区域规划为开发区，除其中4 km2的水塘外，均作为建筑或绿化用地，试求这个开发区的建筑及绿化用地的面积是多少？
粤公网安备 44130202000953号