小亮家距离学校8千米，昨天早晨，小亮骑车上学途中，自行车“爆胎”，恰好路边有“自行车”维修部，几分钟后车修好了，为了不迟到，他加快了骑车到校的速度．回校后，小亮根据这段经历画出如下图象．该图象描绘了小亮行的路程S与他所用的时间t之间的关系．请根据图象，解答下列问题：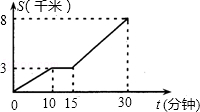
（1）小亮行了多少千米时，自行车“爆胎”？修车用了几分钟？
（2）小亮到校路上共用了多少时间？
（3）如果自行车没有“爆胎”，一直用修车前的速度行驶，那么他比实际情况早到或晚到学校多少分钟（精确到0.1）？
相关试题
如图，在⊙O中，AB、CD是两条弦，OE⊥AB，OF⊥CD，垂足分别为E、F．
（1）如果∠AOB=∠COD，那么OE与OF的大小有什么关系？为什么？
（2）如果OE=OF，那么
与
的大小有什么关系？为什么？
如图，O是正六边形ABCDEF的中心，连接BD、DF、FB，
（1）设△BDF的面积为S1，正六边形ABCDEF的面积为S2 ，则S1与S2的数量关系是 ；
（2）△ABF通过旋转可与△CDB重合，请指出旋转中心和最小旋转角的度数．
如图，⊙M经过O点，并且⊙M与x轴，y轴分别交于A，B两点，线段OA，OB（OA＞OB）的长是方程
的两根．
（1）求线段OA，OB的长；
（2）已知点C是劣弧
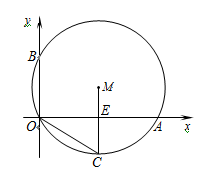
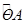的中点，连结MC交OA轴于点E．
①判断MC与OA的位置关系，并说明理由；
②求点C的坐标．
相关知识点
推荐套卷
粤公网安备 44130202000953号