已知圆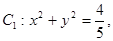
直线
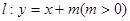与圆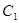
相切，且交椭圆
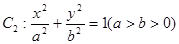于
两点，
是椭圆的半焦距，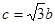
，
（Ⅰ）求
的值；
（Ⅱ）O为坐标原点，若
求椭圆
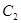的方程；
(Ⅲ) 在（Ⅱ）的条件下，设椭圆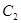的左右顶点分别为A，B，动点
，直线AS，BS与直线
分别交于M,N两点，求线段MN的长度的最小值.
，|2x－y|＜
，求证：|y|＜
.
，求矩阵A的特征值．
，B＝
，求矩阵A－1B.推荐套卷
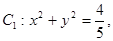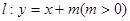已知圆直线与圆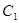相切，且交椭圆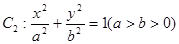于两点，是椭圆的半焦距，，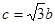
（Ⅰ）求的值；
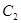（Ⅱ）O为坐标原点，若求椭圆的方程；
(Ⅲ) 在（Ⅱ）的条件下，设椭圆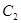的左右顶点分别为A，B，动点，直线AS，BS与直线分别交于M,N两点，求线段MN的长度的最小值.
粤公网安备 44130202000953号