设等比数列 的首项为
的首项为 ,公比为
,公比为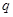 (
(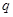 为正整数),且满足
为正整数),且满足 是
是 与
与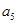 的等差中项;数列
的等差中项;数列 满足
满足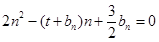 (
(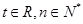 ).
).
(1)求数列 的通项公式;
的通项公式;
(2)试确定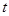 的值,使得数列
的值,使得数列 为等差数列;
为等差数列;
(3)当 为等差数列时,对每个正整数
为等差数列时,对每个正整数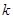 ,在
,在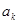 与
与 之间插入
之间插入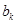 个2,得到一个新数列
个2,得到一个新数列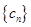 . 设
. 设 是数列
是数列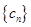 的前
的前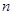 项和,试求满足
项和,试求满足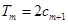 的所有正整数
的所有正整数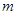 .
.
相关知识点
推荐套卷
设等比数列 的首项为
的首项为 ,公比为
,公比为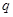 (
(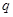 为正整数),且满足
为正整数),且满足 是
是 与
与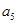 的等差中项;数列
的等差中项;数列 满足
满足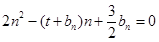 (
(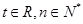 ).
).
(1)求数列 的通项公式;
的通项公式;
(2)试确定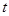 的值,使得数列
的值,使得数列 为等差数列;
为等差数列;
(3)当 为等差数列时,对每个正整数
为等差数列时,对每个正整数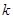 ,在
,在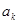 与
与 之间插入
之间插入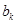 个2,得到一个新数列
个2,得到一个新数列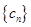 . 设
. 设 是数列
是数列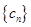 的前
的前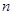 项和,试求满足
项和,试求满足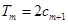 的所有正整数
的所有正整数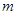 .
.