如果我们定义:“到三角形的两个顶点距离相等的点,叫做此三角形的开心点。”那么: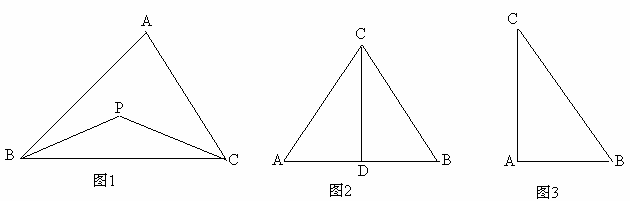
(1)如图1,观察并思考,△ABC的开心点有 个
(2)如图2,CD为等边三角形ABC的高,开心点P在高CD上,且PD=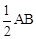 ,则∠APB的度数为
,则∠APB的度数为
(3)已知△ABC为直角三角形,斜边BC=5,AB=3,开心点P在AC边上,试探究PA的长。
相关知识点
推荐套卷
如果我们定义:“到三角形的两个顶点距离相等的点,叫做此三角形的开心点。”那么:
(1)如图1,观察并思考,△ABC的开心点有 个
(2)如图2,CD为等边三角形ABC的高,开心点P在高CD上,且PD=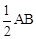 ,则∠APB的度数为
,则∠APB的度数为
(3)已知△ABC为直角三角形,斜边BC=5,AB=3,开心点P在AC边上,试探究PA的长。