如图：在等腰梯形ABCD中，AB＝DC＝5，AD＝4，BC＝10．点E在下底边BC上，点F在腰AB上．
①、则梯形的高是 ；
②、若EF平分等腰梯形ABCD的周长，设BE长为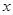
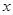，试用含的代数式表示△BEF的面积；
③、是否存在线段EF将等腰梯形ABCD的周长和面积同时平分？若存在，求出此BE的长；若不存在，请说明理由；
④、是否存在线段EF将等腰梯形ABCD的周长和面积同时分成1︰2的两部分？若存在，求此时BE的长；若不存在，请说明理由．
相关试题
生活中的数学（共10分）（1）小明同学在某月的日历上圈出2×2个数（如图），正方形方框内的4个数的和是28，那么这4个数是
（2）小丽同学在日历上圈出5个数，呈十字框型（如图），他们的和是65，则正中间一个数是
（3）某月有5个星期日，这5个星期日的日期之和为80，则这个月中第一星期日的日期是号。
（4）有一个数列每行8个数成一定规律排列如图：
①图中方框内的9个数的和是
②小刚同学在这个数列上圈了一个斜框（如图），圈出的9个数的和为522，求正中间的一个数。
（共10分）（1）当a = -2，b=1时，求两个代数式（a+b）2与a2+2ab+b2的值；
（2）当a =-2，b= -3时，再求以上两个代数式的值；
（3）你能从上面的计算结果中，发现上面有什么结论？
结论是：；（4）利用你发现的结论，求：19652+1965×70+352的值．
、
，定义运算：“
”，
（填“＞”或“＝”或“＜”）；我们知道：有理数的加法运算和乘法运算满足交换律.那么，由以上计算的结果进行猜想：“相关知识点
推荐套卷
粤公网安备 44130202000953号