某地开发了一个旅游景点,第1年的游客约为100万人,第2年的游客约为120万人.某数学兴趣小组综合各种因素预测:①该景点每年的游客人数会逐年增加;②该景点每年的游客都达不到130万人.该兴趣小组想找一个函数 来拟合该景点对外开放的第
来拟合该景点对外开放的第
 年与当年的游客人数
年与当年的游客人数 (单位:万人)之间的关系.
(单位:万人)之间的关系.
(1)根据上述两点预测,请用数学语言描述函数 所具有的性质;
所具有的性质;
(2)若 =
= ,试确定
,试确定 的值,并考察该函数是否符合上述两点预测;
的值,并考察该函数是否符合上述两点预测;
(3)若 =
= ,欲使得该函数符合上述两点预测,试确定
,欲使得该函数符合上述两点预测,试确定 的取值范围.
的取值范围.
相关知识点
推荐套卷
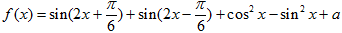 的在区间
的在区间 上的最小值为0.
上的最小值为0.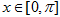 时,求使
时,求使 成立的x的集合.
成立的x的集合.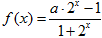 是实数集R上的奇函数.
是实数集R上的奇函数.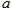 的值;
的值; 在
在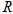 上的单调性并加以证明;
上的单调性并加以证明;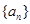 是公比为正数的等比数列,
是公比为正数的等比数列,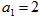 ,
, .
.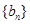 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列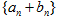 的前
的前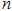 项和
项和 .
. 各项均为正数的数列
各项均为正数的数列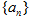 满足
满足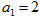 ,
, ,
, .
. 是等比数列;
是等比数列;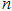 取何值时,
取何值时, 取最大值,并求出最大值;
取最大值,并求出最大值; 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.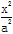 +
+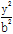 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为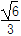 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为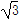 .
. ,求△AOB面积的最大值.
,求△AOB面积的最大值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号