（本小题满分16分）已知的三个顶点，，，其外接圆为圆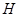
．
（1）若直线过点，且被圆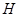截得的弦长为2，求直线的方程；
（2）对于线段上的任意一点，若在以为圆心的圆上都存在不同的两点，使得点是线段的中点，求圆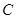
的半径的取值范围．
，
（
）分别对应向量，
（O为原点），若向量
对应的复数为纯虚数，求
的值．
，
，
，它们在复平面上的对应点是一个正方形的三个顶点，求这个正方形的第四个顶点对应的复数。
，
，求证：
求证：
，
中至少有一个是1．
，
，试求
相关知识点
推荐套卷
（本小题满分16分）已知的三个顶点，，，其外接圆为圆．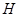
（1）若直线过点，且被圆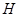截得的弦长为2，求直线的方程；
（2）对于线段上的任意一点，若在以为圆心的圆上都存在不同的两点，使得点是线段的中点，求圆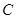的半径的取值范围．
粤公网安备 44130202000953号