已知真命题:“函数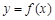 的图像关于点
的图像关于点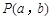 成中心对称图形”的充要条件为“函数
成中心对称图形”的充要条件为“函数 是奇函数”.
是奇函数”.
(Ⅰ)将函数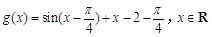 的图像向左平移
的图像向左平移 个单位,再向上平移2个单位,求此时图像对应的函数解析式,并利用题设中的真命题求函数
个单位,再向上平移2个单位,求此时图像对应的函数解析式,并利用题设中的真命题求函数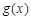 图像对称中心的坐标;
图像对称中心的坐标;
(Ⅱ)求函数 图像对称中心的坐标;
图像对称中心的坐标;
(Ⅲ)已知命题:“函数 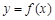 的图像关于某直线成轴对称图像”的充要条件为“存在实数
的图像关于某直线成轴对称图像”的充要条件为“存在实数 和
和 ,使得函数
,使得函数 是偶函数”.判断该命题的真假,如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).
是偶函数”.判断该命题的真假,如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).
推荐套卷
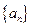 满足
满足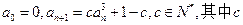 为实数
为实数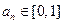 对任意
对任意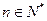 成立的充分必要条件是
成立的充分必要条件是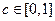 ;
;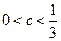 ,证明:
,证明: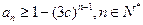 ;
;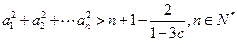
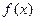 和数列
和数列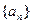 满足下列条件:
满足下列条件: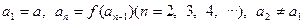 ,
,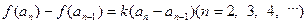 ,其中a为常数,k为非零常数.
,其中a为常数,k为非零常数.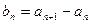
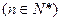 ,证明数列
,证明数列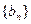 是等比数列;
是等比数列;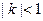 时,求
时,求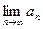 .
.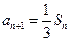 ,n=1,2,3,……,求
,n=1,2,3,……,求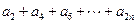 的值.
的值.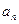 }是公比为q的等比数列,且
}是公比为q的等比数列,且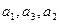 成等差数列.
成等差数列.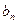 }是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
}是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.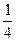 ,且
,且 ,
,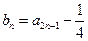 ,n==l,2,3,…·.
,n==l,2,3,…·.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号