对某校高一年级学生参加社区服务次数统计，随机抽取了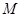
名学生作为样本，得到这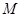名学生参加社区服务的次数，根据此数据作出了频数与频率的统计表如下：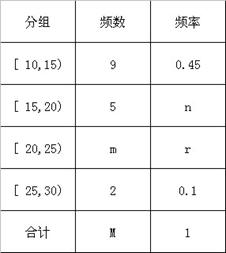
（1）求出表中
的值；
（2）在所取样本中，从参加社区服务的次数不少于
次的学生中任选
人，求至少一人参加社区服务次数在区间
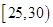内的概率．
，并说明理由.
的不等式
（
，且
）.
的值。
.
； (2)求
；（3）求
.推荐套卷
对某校高一年级学生参加社区服务次数统计，随机抽取了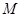名学生作为样本，得到这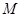名学生参加社区服务的次数，根据此数据作出了频数与频率的统计表如下：
（1）求出表中的值；
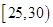（2）在所取样本中，从参加社区服务的次数不少于次的学生中任选人，求至少一人参加社区服务次数在区间内的概率．
粤公网安备 44130202000953号