一个袋子中装有6个红球和4个白球，假设每一个球被摸到的可能性是相等的.
（Ⅰ）从袋子中摸出3个球，求摸出的球为2个红球和1个白球的概率；
（Ⅱ）从袋子中摸出两个球，其中白球的个数为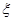
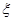，求的分布列和数学期望.
）.若
，且
，求角
的大小；
，
，函数
，若
且
，求
的值；
)的值；
∈(0，
)，f (
)＝
，求cos2
相关知识点
推荐套卷
一个袋子中装有6个红球和4个白球，假设每一个球被摸到的可能性是相等的.
（Ⅰ）从袋子中摸出3个球，求摸出的球为2个红球和1个白球的概率；
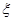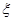（Ⅱ）从袋子中摸出两个球，其中白球的个数为，求的分布列和数学期望.
粤公网安备 44130202000953号