某数学老师对本校2013届高三学生某次联考的数学成绩进行分析，按1:50进行分层抽样抽取的20名学生的成绩进行分析，分数用茎叶图记录如下：
得到频率分步表如下：
（1）求表中
的值，并估计这次考试全校学生数学成绩及格率（分数在
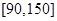范围为及格）；
（2）从大于等于110分的学生中随机选2名学生得分，求2名学生的平均得分大于等于130分的概率.
相关试题
.
在点
处与直线
相切，求
的值；
的单调区间与极值点。
中，
已知
分别为等差数列
的第3项和第5项，试求数列
公式及前
项和
。
中，
为锐角，角
所对的边分别为
，且
的值；
，求
为平行四边形
所在平面外一点，
为
的中点，
平面
．
和
轴相切，圆心在直线
上，且被直线
截得的弦长为
，求圆
相关知识点
推荐套卷
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析，按1:50进行分层抽样抽取的20名学生的成绩进行分析，分数用茎叶图记录如下：
得到频率分步表如下：
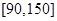（1）求表中的值，并估计这次考试全校学生数学成绩及格率（分数在范围为及格）；
（2）从大于等于110分的学生中随机选2名学生得分，求2名学生的平均得分大于等于130分的概率.
粤公网安备 44130202000953号