已知二次函数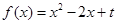
与两坐标轴分别交于不同的三点A、B、C.
（1）求实数t的取值范围；
（2）当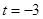
时，求经过A、B、C三点的圆F的方程；
（3）过原点作两条相互垂直的直线分别交圆F于M、N、P、Q四点，求四边形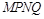
的面积的最大值。
,求实数
的值；
，求实数
中，
，
.
，证明
是等比数列；
，求数列
的前
项和
.
的不等式
.
为等差数列，
是等差数列的前
项和，已知
，
.
；
为数列
的前
的三个内角
所对的边分别为
,且满足
.
的大小；
，
，求
的值.推荐套卷
已知二次函数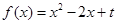与两坐标轴分别交于不同的三点A、B、C.
（1）求实数t的取值范围；
（2）当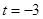时，求经过A、B、C三点的圆F的方程；
（3）过原点作两条相互垂直的直线分别交圆F于M、N、P、Q四点，求四边形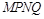的面积的最大值。
粤公网安备 44130202000953号