为了解甲、乙两厂产品的质量,从两厂生产的产品中分别随机抽取各10件样品,测量产品中某种元素的含量(单位:毫克).如图是测量数据的茎叶图: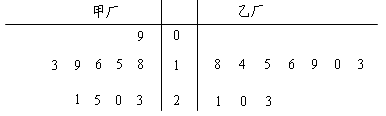
规定:当产品中的此种元素含量不小于18毫克时,该产品为优等品.
(1)试用上述样本数据估计甲、乙两厂生产的优等品率;
(2)从乙厂抽出的上述10件样品中,随机抽取3件,求抽到的3件样品中优等品数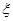 的分布列及其数学期望
的分布列及其数学期望 ;
;
(3)从甲厂的10件样品中有放回的随机抽取3件,也从乙厂的10件样品中有放回的随机抽取3件,求抽到的优等品数甲厂恰比乙厂多2件的概率.
相关知识点
推荐套卷
 ,(其中
,(其中 )
) 及
及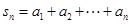 ;
; 与
与 的大小,并说明理由.
的大小,并说明理由. 分,海选不合格记
分,海选不合格记 分.假设甲、乙、丙海选合格的概率分别为
分.假设甲、乙、丙海选合格的概率分别为 ,他们海选合格与不合格是相互独立的.
,他们海选合格与不合格是相互独立的. ,求随机变量
,求随机变量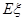 .
.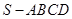 的高为
的高为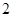 ,底面
,底面 是边长为
是边长为 的正方形,顶点
的正方形,顶点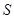 在底面上的射影是正方形
在底面上的射影是正方形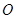 .
.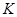 是棱
是棱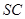 的中点.试求直线
的中点.试求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
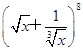 的展开式中二项式系数最大项.
的展开式中二项式系数最大项. 在
在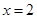 时取得极小值.
时取得极小值. 的值;
的值; ,使得
,使得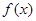 在该区间上的值域为
在该区间上的值域为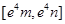 ?若存在,求出
?若存在,求出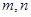 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号