如图，一次函数
的图象与x轴、y轴分别相交于点A、B．P是射线BO上的一个动点（点P不与点B重合），过点P作PC⊥AB，垂足为C，在射线CA上截取CD=CP，连接PD．设BP=t．
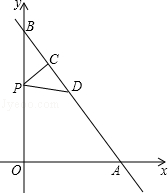
（1）t为何值时，点D恰好与点A重合？
（2）设△PCD与△AOB重叠部分的面积为S，求S与t的函数关系式，并直接写出t的取值范围．
，求
的值．
=4，求a2+
和a4+
的值．相关知识点
推荐套卷
如图，一次函数的图象与x轴、y轴分别相交于点A、B．P是射线BO上的一个动点（点P不与点B重合），过点P作PC⊥AB，垂足为C，在射线CA上截取CD=CP，连接PD．设BP=t．
（1）t为何值时，点D恰好与点A重合？
（2）设△PCD与△AOB重叠部分的面积为S，求S与t的函数关系式，并直接写出t的取值范围．
粤公网安备 44130202000953号