已知无穷数列 中,
中, 、
、 、
、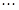 、
、 构成首项为2,公差为-2的等差数列,
构成首项为2,公差为-2的等差数列,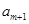 、
、 、
、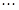 、
、 ,构成首项为
,构成首项为 ,公比为
,公比为 的等比数列,其中
的等比数列,其中 ,
,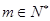 .
.
(1)当 ,
,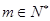 ,时,求数列
,时,求数列 的通项公式;
的通项公式;
(2)若对任意的 ,都有
,都有 成立.
成立.
①当 时,求
时,求 的值;
的值;
②记数列 的前
的前 项和为
项和为 .判断是否存在
.判断是否存在 ,使得
,使得 成立?若存在,求出
成立?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
相关知识点
推荐套卷
已知无穷数列 中,
中, 、
、 、
、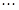 、
、 构成首项为2,公差为-2的等差数列,
构成首项为2,公差为-2的等差数列,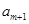 、
、 、
、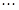 、
、 ,构成首项为
,构成首项为 ,公比为
,公比为 的等比数列,其中
的等比数列,其中 ,
,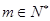 .
.
(1)当 ,
,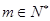 ,时,求数列
,时,求数列 的通项公式;
的通项公式;
(2)若对任意的 ,都有
,都有 成立.
成立.
①当 时,求
时,求 的值;
的值;
②记数列 的前
的前 项和为
项和为 .判断是否存在
.判断是否存在 ,使得
,使得 成立?若存在,求出
成立?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.