如图，直线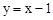
与反比例函数
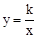的图象交于A、B两点，与x轴交于点C，已知点A的坐标为（－1，m）．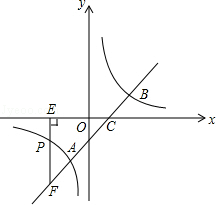
（1）求反比例函数的解析式；
（2）若点P（n，1）是反比例函数图象上一点，过点P作PE⊥x轴于点E，延长EP交直线AB于点F，求△CEF的面积．
相关试题
和
，你能找到一个合适的
值，使它们的值相等吗？写出你的解题过程.
，求
的值。
相关知识点
推荐套卷
如图，直线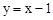与反比例函数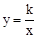的图象交于A、B两点，与x轴交于点C，已知点A的坐标为（－1，m）．
（1）求反比例函数的解析式；
（2）若点P（n，1）是反比例函数图象上一点，过点P作PE⊥x轴于点E，延长EP交直线AB于点F，求△CEF的面积．
粤公网安备 44130202000953号