如图1，点C、B分别为抛物线C1：y1＝x2＋1，抛物线C2：y2＝a2x2＋b2x＋c2的顶点．分别过点B、C作x轴的平行线，交抛物线C1、C2于点A、D，且AB＝BD．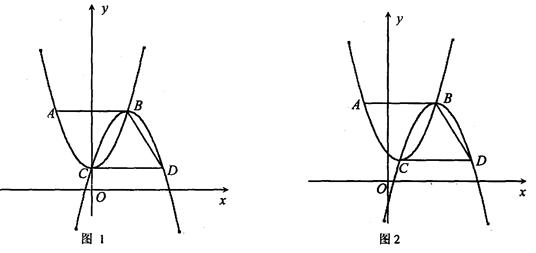
(1)求点A的坐标：
(2)如图2，若将抛物线C1：“y1＝x2＋1”改为抛物线“y1＝2x2＋b1x＋c1”．其他条件不变，求CD的长和a2的值；
(3)如图2，若将抛物线C1：“y1＝x2＋1”改
为抛物线“y1＝4x2＋b1x＋c1”，其他条件不变，求b1＋b2的值 ▲ （直接写结果）．
相关试题
，
；（2）
如图，已知反比例函数
和一次函数
的图象相交于第一象限内的点A，且点A的横坐标为1。过点A作AB⊥x轴于点B，△AOB的面积为1。
（1）求反比例函数和一次函数的解析式；
（2）若一次函数的图象与x轴相交于点C，求线段AC的长度；
（3）直接写出：当
＞
＞0时，x的取值范围；
（4）在y轴上是否存在一点p，使△PAO为等腰三角形，若存在，请直接写出p点坐标，若不存在，请说明理由。（要求至少写两个）
相关知识点
推荐套卷
粤公网安备 44130202000953号