如图,已知抛物线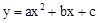 经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.
经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.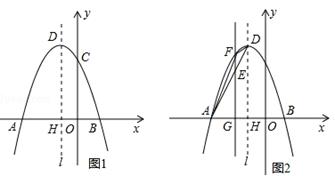
(1)求该抛物线的解析式;
(2)若点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值;
(3)如图(2),若E是线段AD上的一个动点( E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.
①求S与m的函数关系式;
②S是否存在最大值?若存在,求出最大值及此时点E的坐标; 若不存在,请说明理由.
相关知识点
推荐套卷
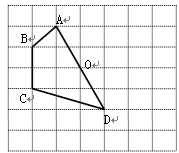
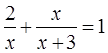

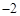 )=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移
)=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移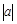 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移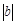 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为 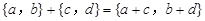 .
.
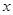 件,月总收入为
件,月总收入为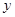 元,销售每件奖励
元,销售每件奖励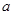 元,营业员月基本工资为
元,营业员月基本工资为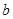 元.
元. 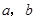 的值;
的值;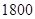 元,那么小俐当月至少要卖服装多少件?
元,那么小俐当月至少要卖服装多少件? 粤公网安备 44130202000953号
粤公网安备 44130202000953号