如图,在平面直角坐标系中,有一条直线l: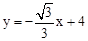 与x轴、y轴分别交于点M、N,一个高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移.
与x轴、y轴分别交于点M、N,一个高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移.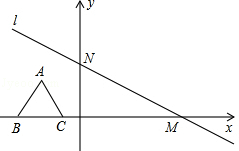
(1)在平移过程中,得到△A1B1C1,此时顶点A1恰落在直线l上,写出A1点的坐标 ;
(2)继续向右平移,得到△A2B2C2,此时它的外心P恰好落在直线l上,求P点的坐标;
(3)在直线l上是否存在这样的点,与(2)中的A2、B2、C2任意两点能同时构成三个等腰三角形?如果存在,求出点的坐标;如果不存在,说明理由.
相关知识点
推荐套卷
 中,A、B为x轴上两点,C、D为y轴上的两点,经
中,A、B为x轴上两点,C、D为y轴上的两点,经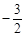 ),点M是抛物线C2:
),点M是抛物线C2: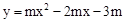 (
(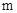 <0)的顶点.
<0)的顶点.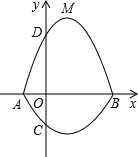
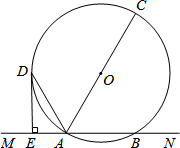
 的图象与一次函数
的图象与一次函数 的图象交于点A(1,4)和点B
的图象交于点A(1,4)和点B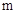 ,
,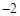 ).
).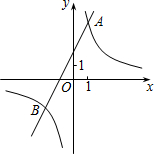
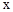 >0时,直接写出
>0时,直接写出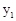 >
> 时自变量
时自变量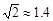 ,
, ,结果保留整数.)
,结果保留整数.)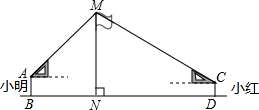
 粤公网安备 44130202000953号
粤公网安备 44130202000953号