已知各项均为正数的两个无穷数列 、
、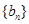 满足
满足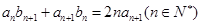 .
.
(Ⅰ)当数列 是常数列(各项都相等的数列),且
是常数列(各项都相等的数列),且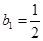 时,求数列
时,求数列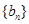 的通项公式;
的通项公式;
(Ⅱ)设 、
、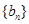 都是公差不为0的等差数列,求证:数列
都是公差不为0的等差数列,求证:数列 有无穷多个,而数列
有无穷多个,而数列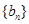 惟一确定;
惟一确定;
(Ⅲ)设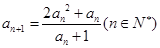 ,
,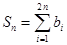 ,求证:
,求证: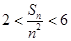 .
.
推荐套卷
已知各项均为正数的两个无穷数列 、
、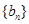 满足
满足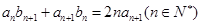 .
.
(Ⅰ)当数列 是常数列(各项都相等的数列),且
是常数列(各项都相等的数列),且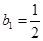 时,求数列
时,求数列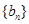 的通项公式;
的通项公式;
(Ⅱ)设 、
、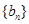 都是公差不为0的等差数列,求证:数列
都是公差不为0的等差数列,求证:数列 有无穷多个,而数列
有无穷多个,而数列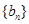 惟一确定;
惟一确定;
(Ⅲ)设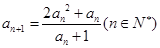 ,
,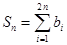 ,求证:
,求证: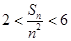 .
.